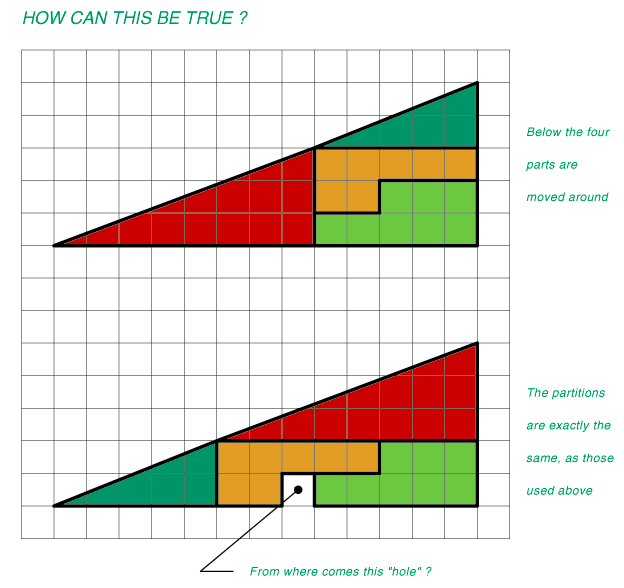
4. Here is one I sent Terry. I think the graph gives it away - others disagree and went on to do trigonometry (HA!!).
TRIBUTE TO TERRY TROTTER - A TRUE PYTHAGOREAN - A MATHEMATIKOI - A WONDERFUL SHARING AND LOVING PERSON WHO FOUND JOY AND HUMOR IN MATH AND SHARED SOME OF IT.
Tribute from T. Marsh
More on Terry Trotter can be found at his site, which was up at the time of writing.
( http://www.teherba.org/trottermath.net/ ) I had to update the site, which might be updated again to add the "https".
On January 28, 2005, I was informed that Terry passed away on September 29, 2004. The Math Forum had a tribute up for him, but they took it down shortly after. I wish to keep a tribute up for Terry and since there is room on this website, I'm putting it here.
This below is the first thing I ever saw from Terry - extremely entertaining. While the problems are not hard to do (you must do them to see what's strange about the numbers) - I think that figuring out that there is this strangeness in these numbers is hard. His entire website is amazing and filled with wonderful things about numbers - but this below was the first thing I ever saw from Terry. From then on, we exchanged math problems and puzzles.
ENJOY!
STRANGE THINGS THAT HAPPEN WITH NUMBERS - Terry Trotter, Mathematician.
1. Arrange the first eight digits in order, like this: 1, 2, 3, 4 and 5, 6, 7, 8 Now, we can add some symbols to make true facts: 12 = 3 x 4 and 56 = 7 x 8 2. It is possible to make true and complete multiplication problems (that is, make the factors AND the product) in the two following unusual ways: a) Use only the first five digits once and only once; that is, 1, 2, 3, 4, and 5. b) Use only the first five odd digits once and only once; that is, 1, 3, 5, 7, and 9. Can you find the whole problem for each case? 3. Multiply 21978 by 4; then look at your answer to see a strange thing. 4. Multiply 10989 by 9; then look at your answer to see a strange thing. 5. Multiply 421,052,631,578,947,368 by 2; then look at your answer to see a strange thing. 6. Take the digits 1, 2, and 3 and make all the two-place numbers possible; use each digit only once per number. (There will be six such numbers.) Add up these numbers to see a strange thing. Do the same again, first using the digits 2, 4, and 6. Then try 3, 6, and 9. Will this happen with any three different digits? (No, there are no more in the 3-digit range.) 7. The year 1962 was a strange year. To see just how strange, do the following steps as directed: a) Find 1/2 (one-half) of 1962; it = __________. b) Find 1/3 (one-third) of 1962; it = __________. c) Find 1/6 (one-sixth) of 1962; it = __________. d) Add those three answers here.----> __________. For an added strange bonus look at the individual digits that were in your three addends (a, b, and c).Part II 1. Write the first ten prime numbers in order, as shown (Note: the 11 is used twice): 2, 3, 5, 7, 11 11, 13, 17, 19, 23, 29 Now, by putting in some symbols for multiplication, addition, and squaring, we have 2 x 3 x 5 x 7 x 11 11^2 + 13^2 + 17^2 + 19^2 + 23^2 + 29^2 Figure out the two parts to see which side is larger in value. 2. Multiply 11,826 by itself and look at your answer to see a strange thing. The same strange thing also happens with 30,384. But just what is the product anyway? 3. Take the number 153. Find the cube (3rd power) of each of the three digits. Add up these three values to see a strange thing. The same strange thing also happens with these numbers: 370, 371, and 407. Can you find any more? 4. Now we will try the same sort of thing with the following numbers. BUT this time you are to first find the fourth power of each digit before adding. (Warning: only some of the numbers below actually work. Which ones are they?) a) 1634 b) 2451 c) 8208 d) 9474 e) 5072 5. Do you want to go for fifth powers now? Okay, good. First, find the fifth power of each digit, then add up the resulting values. (Gee, aren't numbers strange acting sometimes?) a) 4150 b) 54,748 c) 22,132 d) 4151 e) 1145 Did they all work, or not?Part III 1. Find the values of the following powers. Then add up the digits of the final product to see a strange thing. a) 17^3 b) 18^3 c) 27^3 d) 26^3 (As an example of this idea, use 8^3. 8^3 = 512 and 5 + 1 + 2 = 8. Do you see it now?) Strange as this may be, it can even work with certain fourth powers, too. Try it with 7, 22, and 25. Would you believe FIFTH powers, too? By now, you'll probably believe anything, right? Well, it's true! Try it with these numbers: 28 and 35. 2. There is something very strange about these pairs of consecutive numbers. To see what it is, first find the squares of each one in the pair, then look closely at the digits in the products. Strange, isn't it? a) 13 & 14 b) 157 & 158 c) 913 & 914 3. On we go with more strange things...these are rather easy. Just perform the indicated operations. Then compare your final answer with what you started with. a) 12^2 + 33^2 = b) 88^2 + 33^2 = c) 10^2 + 100^2 = d) 588^2 + 2353^2 = 4. Here's a weird one, for sure. Pay careful attention now. First, do the multiplication problems that are below. Then, reverse the big factor (the 5-place number) and try to find a one-place number that when it and the reversed factor are multiplied, you get the same product that you found the first time. Try it---it's not so bad afterall. a) 10989 x 9 = d) 43956 x 6 = b) 21978 x 8 = e) 54945 x 5 = c) 32967 x 7 =Part IV 1. Here is another strange thing that involves all nine digits from 1 to 9. If you find the square of 567, the product will contain only the six other digits (1, 2, 3, 4, 8, and 9). But, what is that product? The same kind of thing happens with 854. What is the six- digit square number this time? 2. The square of 428 is 183,184. This product has the strange property that if the six digits are separated into two halves, we have the consecutive 3-place numbers 183 and 184. This is a rare thing, to be sure. In fact, the only numbers whose squares have this property are mixed into the list of numbers below. Some of them work; some don't. So, tell me which ones work, and give the strange product. 573 625 727 846 904 3. Study this true number sentence for a moment: 1 + 2 + 6 = 4 + 5 Now, believe it or not, if we square each number, then add, both sides will STILL be equal! Look... 1^2 + 2^2 + 6^2 = 4^2 + 5^2 1 + 4 + 36 = 16 + 25 41 = 41 That, you will have to admit, is rather strange. Of course, by now you know these strange things just don't happen all the time. So, below you will find several true number sentences. BUT the square number versions may or may not be like the example above. So, for those that are true both ways, show me why they are (that is, find the squares and the equal totals). 1 + 8 + 9 = 3 + 4 + 11 7 + 9 + 12 = 6 + 10 + 13 2 + 7 + 10 = 4 + 6 + 9 2 + 7 + 9 = 3 + 5 + 10 1 + 5 + 7 + 9 = 2 + 4 + 6 + 10 5 + 7 + 7 + 8 = 3 + 4 + 6 + 14 1 + 5 + 8 + 12 = 2 + 3 + 10 + 11Part V 1. Try this. Pick the name of any number you wish. Count the number of letters that are in it. Write that number as a word again. Do the counting part again. Keep on doing this until a surprise strikes you. Here is an example to explain the idea: THIRTY-THREE ==> ELEVEN ==> SIX ==> (go on...) Do this with at least five different number names. Be sure to try some "BIG" numbers. What result(s) do you find? 2. Pick any number. If it is even, cut it in half (divide by 2). If it is odd, multiply it by 3, then add 1. Continue with these two rules with each new answer you get, until a surprise shows up. Here are two examples: a) 13 ==> 40 ==> 20 ==> 10 ==> 5 ==> 16 ==> (go on...) b) 106 ==> 53 ==> 160 ==> 80 ==> (go on...) Do this with five more numbers that you choose. What result(s) do you find? 3. Pick any number. Find the square of each of its digits; then add those digits. Take the sum and continue the process, over and over, until a surprise shows up. Here are two examples: a) 18 1 36 36 9 25 + 64 + 25 + 1 + 49 + 64 (go on...) 65 61 37 58 89 b) 1333 1 4 36 9 + 64 + 64 (go on...) 9 68 100 + 9 28 Do this process with these six numbers and tell what results you find. Then pick your own number (make it greater than 1000) and do the process on it. A) 92 B) 4208 C) 23 D) 153 E) 54,151 F) 657
*************************************
1. Here is a variation of a problem Terry has on his website. Using the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9, arrange them so that they add up to 100. You have to use every number and you can only use the number one time. You can ONLY add; fractions are OK. (Terry's problem allows other functions.)
2. Here's another one, not from Terry: how can 8 8s equal 1,000?
3. Here is one Terry sent me. If you can do numbers like this in your head, it's pretty fast. Using 3 digit numbers that add up to 12 (like 723), find numbers that fit this qualification:
a. The number itself.b. The number multiplied by 2.c. The number multiplied by 3.When you are done you have in the answers all the numbers from 1 to 9.
Example: the number 192
192 x 2 = 384
192 x 3 = 576You can see that the number, the number x 2 and the number x 3 gives you numbers 1 - 9
FIND MORE!
4. Here is one I sent Terry. I think the graph gives it away - others disagree and went on to do trigonometry (HA!!).
